nticipating tremendous potential, big tech companies and governments are scrambling to be the first to build quantum computing devices. Unlike today’s computers that play only by the rules of classical physics, quantum computing promises a “silver bullet” solution for tasks deemed “incomputable.” This excitement adds to a sustained fascination for quantum physics since its origins more than 100 years ago. Even today, a claim in a paper published in a scientific journal about fundamental quantum waves (or particles) has a good chance of making it into the daily news cycle. This ongoing interest stems from the fact that quantum mechanics lies outside of our personal experience of the natural world and contains philosophically challenging notions that spark debates—even among experts. The current interest in society demands that researchers convey the inner workings of quantum computers through terms in which the public can relate. However, physicists see the abstract world through the lens of mathematical structures—a language not easily translated to a layperson.
Riding the Swell
The conveyance of abstract information via imagery in a way that connects people on a personal level often lies within the realm of artistic expression. Art serves as a visual association of analogous concepts. So, how can we envision quantum physics and quantum computers? For quantum mechanics, two concepts are of key importance. The first is that of particles. These are objects located at a single point in space, “the dog is on the chair,” for example. We intrinsically understand objects (or particles) because we encounter them in our everyday lives.
We also encounter waves, but their use in quantum mechanics is a little different to the waves that we encounter in our daily experience of life. One of the most beautiful mental images we can create for ourselves is one of an ocean wave gently rolling onto a beach. As the wave rolls in, we can observe that its motion extends all the way down the beach and it is not localized at any single point. As a second visualization, you may also have observed how, as waves rush in, the seawater navigates its way around the rocks. Sometimes, when the water meets at a single point, all at once it surges up into a big spray. If you can imagine these scenes at the beach, you now have a feeling for “wave interference.” In terms of water waves, “interference” means that a lot of water turned up in one place having taken multiple different paths. In quantum physics, however, observing a big wave means that the probability of finding an object at that position is high. A big splash means that the object (or “particle”) is almost certain to be discovered within the splash. If the splash happens in a single location, we can then recover a particle, because we are certain that we will find the object at one point in space.
The Answer is in the Splash
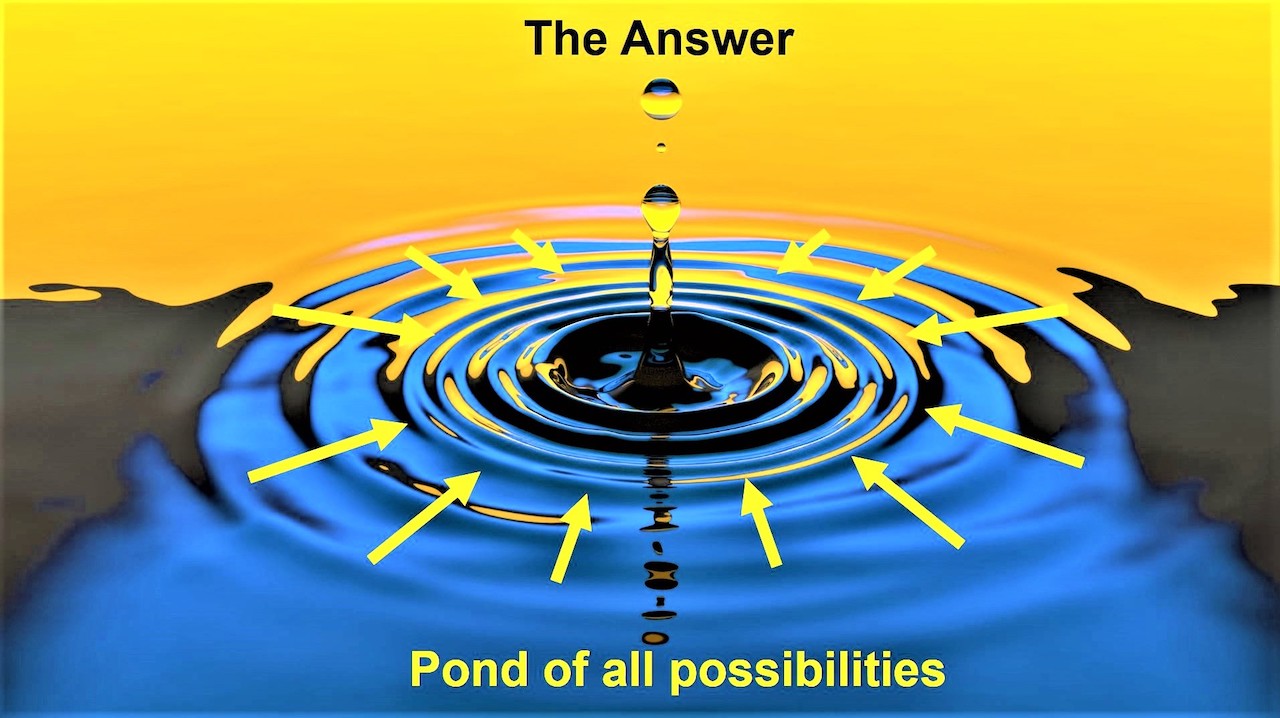
How do waves relate to the function of a quantum computer? Well, in a classical computer (like the one on your desk), there is an organized set of rules. Much like a calculator, classical computers are programmed with a sequence of “yes,” “no,” and “if-then” types of expressions that tell the system to execute certain processes. At any one time, the classical computer is in a fixed configuration (for example labeled by a very long number), and the sequence tells the computer to jump between different configurations. We can view this as a space, where each configuration exits at a particular point in space labeled by its number. The classical computer is then an object that jumps between the different points as the program runs. The number it ends up with is the answer to a problem. Classical computers can also operate by starting at a point that is chosen randomly with some probability (some algorithms find this useful), but they always jump from point to point to point.
The quantum computer is inherently different. In some sense, it manages to occupy all configurations at the same time. It does this by assigning a small probability to each point or configuration, but in quantum physics these probabilities are linked together in a wave-like relationship—much like the relationship that connects all of the water as it rides up the beach. On its own this seems useless, since if we ask the question, “At what point are you?” we get a completely random answer. To make a quantum computer powerful we must instead obtain a specific answer with a very high probability. To do this, an algorithm designer specifies how to make all the different parts of the wave “travel” down different paths (around all of the rocks at the beach), and then combines the parts again to result in interference—a huge splash at a single point in space. If the programmer did the job correctly, the quantum computer “splash” would then select out a single point—the answer to the problem it is trying to solve. Quantum computers thus rely upon wave-like behavior and extract relationships between possibilities. It is no coincidence; therefore, that the heart of many quantum algorithms often involves finding relationships in mathematics. The applications are real and have a significant impact—we anticipate, for example, that quantum computers will break the current cryptographic methods that we use for bank and internet security.
The Beauty of the Wave
The wave property also makes it challenging to build quantum computers. Quantum computers are highly sensitive to anything that disrupts the careful wave relationship that connects the whole of the device. We call this noise, although it does not have to be related to sound—even electrical signals emanating from power lines could constitute noise. Fortunately, theoretical physicists have provided tools that overcome noise disturbances in the form of a beautiful set of ideas that are also intrinsically connected to quantum wave interference and correlations. Realizing these ideas requires greatly improved control of much larger systems than we can currently build. When we get to that point; however, we will finally be able to take full advantage of the quantum world and uncover not just new capabilities in physics, but also apply them to real-world problems. I hope that for all of us, playing and exploring these systems will enable us to understand the essence and beauty of quantum mechanics.


a global affairs media network
How a Walk on the Beach Will Help You Understand Quantum Computing

January 22, 2020
A
nticipating tremendous potential, big tech companies and governments are scrambling to be the first to build quantum computing devices. Unlike today’s computers that play only by the rules of classical physics, quantum computing promises a “silver bullet” solution for tasks deemed “incomputable.” This excitement adds to a sustained fascination for quantum physics since its origins more than 100 years ago. Even today, a claim in a paper published in a scientific journal about fundamental quantum waves (or particles) has a good chance of making it into the daily news cycle. This ongoing interest stems from the fact that quantum mechanics lies outside of our personal experience of the natural world and contains philosophically challenging notions that spark debates—even among experts. The current interest in society demands that researchers convey the inner workings of quantum computers through terms in which the public can relate. However, physicists see the abstract world through the lens of mathematical structures—a language not easily translated to a layperson.
Riding the Swell
The conveyance of abstract information via imagery in a way that connects people on a personal level often lies within the realm of artistic expression. Art serves as a visual association of analogous concepts. So, how can we envision quantum physics and quantum computers? For quantum mechanics, two concepts are of key importance. The first is that of particles. These are objects located at a single point in space, “the dog is on the chair,” for example. We intrinsically understand objects (or particles) because we encounter them in our everyday lives.
We also encounter waves, but their use in quantum mechanics is a little different to the waves that we encounter in our daily experience of life. One of the most beautiful mental images we can create for ourselves is one of an ocean wave gently rolling onto a beach. As the wave rolls in, we can observe that its motion extends all the way down the beach and it is not localized at any single point. As a second visualization, you may also have observed how, as waves rush in, the seawater navigates its way around the rocks. Sometimes, when the water meets at a single point, all at once it surges up into a big spray. If you can imagine these scenes at the beach, you now have a feeling for “wave interference.” In terms of water waves, “interference” means that a lot of water turned up in one place having taken multiple different paths. In quantum physics, however, observing a big wave means that the probability of finding an object at that position is high. A big splash means that the object (or “particle”) is almost certain to be discovered within the splash. If the splash happens in a single location, we can then recover a particle, because we are certain that we will find the object at one point in space.
The Answer is in the Splash

How do waves relate to the function of a quantum computer? Well, in a classical computer (like the one on your desk), there is an organized set of rules. Much like a calculator, classical computers are programmed with a sequence of “yes,” “no,” and “if-then” types of expressions that tell the system to execute certain processes. At any one time, the classical computer is in a fixed configuration (for example labeled by a very long number), and the sequence tells the computer to jump between different configurations. We can view this as a space, where each configuration exits at a particular point in space labeled by its number. The classical computer is then an object that jumps between the different points as the program runs. The number it ends up with is the answer to a problem. Classical computers can also operate by starting at a point that is chosen randomly with some probability (some algorithms find this useful), but they always jump from point to point to point.
The quantum computer is inherently different. In some sense, it manages to occupy all configurations at the same time. It does this by assigning a small probability to each point or configuration, but in quantum physics these probabilities are linked together in a wave-like relationship—much like the relationship that connects all of the water as it rides up the beach. On its own this seems useless, since if we ask the question, “At what point are you?” we get a completely random answer. To make a quantum computer powerful we must instead obtain a specific answer with a very high probability. To do this, an algorithm designer specifies how to make all the different parts of the wave “travel” down different paths (around all of the rocks at the beach), and then combines the parts again to result in interference—a huge splash at a single point in space. If the programmer did the job correctly, the quantum computer “splash” would then select out a single point—the answer to the problem it is trying to solve. Quantum computers thus rely upon wave-like behavior and extract relationships between possibilities. It is no coincidence; therefore, that the heart of many quantum algorithms often involves finding relationships in mathematics. The applications are real and have a significant impact—we anticipate, for example, that quantum computers will break the current cryptographic methods that we use for bank and internet security.
The Beauty of the Wave
The wave property also makes it challenging to build quantum computers. Quantum computers are highly sensitive to anything that disrupts the careful wave relationship that connects the whole of the device. We call this noise, although it does not have to be related to sound—even electrical signals emanating from power lines could constitute noise. Fortunately, theoretical physicists have provided tools that overcome noise disturbances in the form of a beautiful set of ideas that are also intrinsically connected to quantum wave interference and correlations. Realizing these ideas requires greatly improved control of much larger systems than we can currently build. When we get to that point; however, we will finally be able to take full advantage of the quantum world and uncover not just new capabilities in physics, but also apply them to real-world problems. I hope that for all of us, playing and exploring these systems will enable us to understand the essence and beauty of quantum mechanics.


